
|
Moorepage
Projects, info & thoughts from Dick's lab |
|
Most recent update 12-16-2014 Active Twin-T notch filterA path to high-resolution distortion analysis Update — I got some emails.... I designed and built this Active Twin-T filter because I was looking into the distortion performance of ultra-low-distortion oscillators and I wanted to be able to evaluate them throughout the audio range, at least to 20kHz, and also to higher frequencies if possible. So the design described here is fully tunable from 20Hz to 20kHz. Great if you want to evaluate oscillators, but what about other stuff? I have received emails from folks who just want to test other devices, like audio preamps and power amps, and they wanted a somewhat simpler design, with perhaps a few fixed frequencies. Fine, I answered, that can be done, and this article really has all the information buried in it needed to make such a change. But that got me thinking, what's really needed for this? Here's the situation — This Active Twin-T notch filter works in conjunction with some kind of Analog-to-Digital-Converter (ADC) and spectrum analyzer software on a PC. I happen to use two different ADCs: an EMU-0204, and a QuantAsylum QA-400. Both of these units have very good ADC performance but they also include very good Digital-to-Analog-Converters (DACs) too, and these DACs let them output very low distortion sine-wave signals. That capability is of no use in evaluating oscillators, so I didn't dwell on it previously. But for testing audio components, this is extremely useful. Note well that these capabilities are also already built into the sudio functions of most modern computers and in general they work very well, if not quite as well as the outboard components I just mentioned. How low is low? Modern computers now have audio systems that offer 24-bit resolution in both ADCs and DACs, at sample rates as high as 96kHz, and most go to 192kHz. The result is ADC spectrum analysis capabilities that can resolve individual distortion component levels in the mid-band audio range below -100dB (0.001%) and most can even go to -120dB (0.0001%) or more. On the DAC side, the midband (1kHz) products can be well under -90dB, and many can go under -100dB. For most audio testing, the performance of these combined units is more than good enough. Using a spectrum analysis package like ARTA (see link below) lets you connect the DAC output to the ADC input in "loopback" mode to evaluate the best possible performance your computer can deliver. You can see the individual harmonic components, and the package can calculate the Total Harmonic Distortion plus Noise (THD+N) for you automatically. Do you need the Active Twin-T? Only if your gear is truly state-of-the-art — you know, SOTA. I'm not trying to discourage you from building this notch filter, but it's a lot of work to go to if you really don't need it. But, say you do need it — do you need all of its capabilities? Practical realities of testing Any piece of audio gear worth its salt will have distortion at 100Hz or even at 20Hz about as low as at 1kHz, except for possible power supply limitations in power amps or transformer issues in tube gear; and measurements at 20Hz are often hard to make due to power-line related harmonics and noise. So do you need to test down there with the Twin-T? I believe the DAC/ADC testing will give you the info you need at low frequencies, if you need to test there at all, even with SOTA gear — if your results with the Twin-T are great at 1kHz, no reason to do more than check with the basic DAC/ADC audio system at lower frequencies. At higher frequencies, the issues are a bit different. Above 20kHz, the performance of the test oscillator and/or ADC input buffer amp will begin to be an issue, even if they are very good, so at 50kHz or 100kHz, just use the audio system DAC/ADC combo. What's left is testing between 1kHz and 20kHz. So, clearly, testing at (or near) 1kHz is an important qualifier and quantifier of quality in audio gear. From it, results can be inferred about performance in general. Now a couple of options crop up: 1) You can make a Twin-T that works at 1kHz and at 10kHz, which involves (as described in the article below) switching capacitors and using one set (fixed and variable) of resistor values. Or 2) you can test at 1kHz and 20kHz, which again involves switching caps. Or 3) you can test at 2kHz and 20kHz, which is similar to the first option. Or 4) you can test at 1kHz, 10kHz, and 20kHz, the more complicate build, switching both cap sets and resistor sets. I personally like option 1. But many audio designers have followed Bob Cordell's lead and look at the 1kHz to 20kHz distortion ratio as a measure of goodness; for that you need option 4. Now, on to the build... Background Distortion analyzers fall into two main groups -- Total Harmonic Distortion (THD) Analyzers and Spectrum Analyzers (also including Wave Analyzers). The THD Analyzers are represented by units like the famous HP 339A and units from Sound Technology, like the 1701A, and from Tektronix, like the TM AA501A. Spectrum analyzers (and wave analyzers) for audio use are represented by units like the HP 3580A, HP 3581A and the HP 3586A, the Tektronix 7L5, and more recently by units like AP One from Audio Precision; other instrument makers also have units for audio use, like Rhode & Schwartz, and others. All such analyzers use high-Q filters, either band-pass or band-reject, in order to separate the fundamental of a complex signal from its harmonic constituents, which are seen to be non-linearities or impurities in the signal; or to tune to a very narrow band of frequencies in order to isolate and measure the level of one particular frequency. Broadly speaking, the THD analyzers tune out the fundamental and measure some or all of everything in the signal that's left, whereas wave analyzers and spectrum analyzers tune sharply to individual frequency components to measure their frequency and level. Wave analyzers can only look at one spectral component at a time, but many can plot the levels of spectral components by sweeping the hi-Q tuned filter over the range of frequencies of interest. Spectrum analyzers inherently sweep the signal range of interest to make a plot of amplitude(s) vs. frequency. The thing is, such sophisticated instruments can be expensive and may or may not serve to reveal extremely low levels of non-linearity in high-quality audio gear. I encountered this problem directly when I wanted to measure the distortion of an oscillator I was modifying, IG-18 #1. I had on hand an old but very serviceable HP 334A THD Analyzer. Unfortunately, it couldn't measure distortion below about 0.01% at 1kHz, and I was pretty sure the oscillator was better than that. As Paul Klipsch used to say, quoting Barnard's Law, "You can't make what you can't measure, 'cause you don't know when you've got it made." Modern technology has helped folks like me a lot, with computers commonly having pretty decent digital audio capabilities built-in. Naturally, software engineers have made a number of very useful tools to take advantage of these capabilities, including spectrum analyzer software. But I knew from experience that even very good PC sound capabilities, either on-board, as plug-in sound cards, or as USB modules, didn't have the performance to make the kind of measurements I was interested in -- measurements of THD below 0.002%. I tried my project oscillator with a USB sound adaptor from Griffin Technologies called the "iMic" and got very good, but not great results. Was the problem the oscillator, the PC, the analyzer software, or all three? I built another oscillator that I was very sure had great performance, a state-variable design by Bob Cordell. I built that into a second Heath IG-18 chassis, IG-18 #2, the BIG-18. The PC and the iMic measured it at below 0.005%, but the results were equivocal -- noisy and lots of spuriae. I was sure the oscillator was better, and that the problem was the dynamic range of the hardware. Then I discovered that my PC has 24-bit, 96kHz digital sound capability on-board (sound of head hitting wall...), so I settled on using the wonderful ARTA Audio Analysis software. which includes a high-resolution spectrum analyzer function. ARTA and the PC took IG-18 #2 down to THD under 0.002% at 1kHz; that's very good, but was the oscillator actually better? I had to know. I reasoned that if I combined a notch filter with the on-board sound capability and the ARTA software, I could extend the measurement range of the computer to see the distortion products at low levels. Would it work? The Twin-T filter I needed a way to measure very low levels of distortion that was easy and relatively cheap. I wasn't ready then to buy a high-precision THD analyzer or a wave analyzer -- I thought I could cheap out. Years ago I had built a passive Twin-T notch filter tuned to 1kHz to make quick and dirty measurements of amps and oscillators. The Twin-T is the most attractive notch filter from a performance point of view -- it can (with care) be tuned for a notch depth of over 100dB, though the tuning process is a little (!!!) finicky. The trouble is, a) they are hard to tune over a range of frequencies, b) they require numerous adjustable parts for best performance, and c) they attenuate the harmonics of interest to varying degrees, so that you can't easily make a level measurement with an AC voltmeter or scope and know how much correction factor to apply. The typical passive Twin-T filter attenuates the 2nd Harmonic of the tuned frequency by about 9.4dB. That's a lot, and the 3rd H. is attenuated by over 5dB. Accounting for variations in just those two harmonics alone makes precision measurements impossible. The reason for this is that although the notch of the twin-t is very deep, the filter's bandwidth at the -3dB points is too wide; in other words, the Q is too low. Clearly, some form of sharpening of the filter's frequency band is needed. Googling "twin-t filter," for example, will lead you to a number of articles about implementing an active twin-t. The general form of an Active Twin-T filter is shown below. Here, a FET-input opamp U1 buffers the filter and U2 provides the active positive feedback. There is no need for gain adjustment thanks to zero insertion loss. Notch bandwidth, or "Q," is controlled by the ratio of the two Rb resistors -- too sharp and it's hard to tune; too wide and harmonic attenuation is excessive. The 10*Rb value shown is approximate -- an exact ratio will be given below in the schematic. 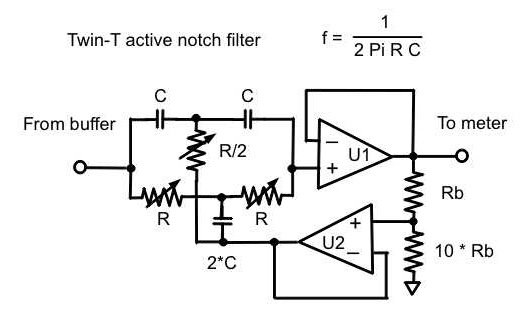 Advantages As shown in the example above, the Twin-T is easily adapted to an active filter design, with feedback to sharpen the notch and thus make correction factors unnecessary. Two sets of switched resistors (large pots don't work well for high resolution due to graininess and large temperature sensitivity) and a small precision pot in each leg (with scaled values) can take the place of the Rs shown below in order to yield high resolution, and with great care and even greater patience, such an analyzer is capable of extremely high levels of performance, well into the range of a few parts per million or even much better. I consider the Twin-T to be the best overall filter type for an active design, despite its relative complexity, because feedback is used only to raise the filter Q -- in other feedback filter forms, which use algebraic summation, feedback is used to tune for both phase and amplitude matching, and my experience has been that this raises low-order distortion products. In fact, all of the summing analyzers I've looked at have fairly high level 2nd Harmonic distortion in the null amplifier. The HP 331-334 series for example have a distortion floor of 0.01% (-80dB) which is due entirely to the level of the 2nd H in the Wien bridge notch filter. Similarly, the HP 339A and the HP 8903 series of analyzers, outstanding instruments, have a measurement floor of about 0.001% (-100dB), again due entirely to the level of the 2nd H. of the summing notch filters they use. I first encountered this form of the Active Twin-T notch filter in an article by John L. Linsley-Hood in Wireless World magazine in the late 1970's. That design stuck with me, so I decided to try and make it work with some of the new quiet, low-distortion opamps that are available, like the Burr-Brown OPA134. I breadboarded a circuit, as described in IG-18 #2. It worked very well, but it was single-frequency only. I needed to be able to tune it. I built the circuit using switched capacitors for the range tuning, and potentiometers for the amplitude tuning elements. It worked, but the carbon composition pots I used were prone to temperature problems, noise, and drift. It works ... mostly I made some measurements and discovered that not only was it hard to tune and impossible to hold on a null, the noise floor of the whole system was hiding distortion components. Checking amplitude linearity with a precision attenuator revealed that levels below -100dB were being compressed by the PC system and giving poor results. On the good side, the filter's attenuation of the 2nd H. was only 0.5dB and the 3rd H. was less than 0.2dB, so I no longer had to worry about accurate measurements of harmonic levels. I decided on a rebuild. The rebuild would have three ranges to cover the 20Hz-20kHz audio band -- 20Hz-200Hz, 200Hz-2kHz, 2kHz-20kHz, giving the coarse tuning a "20" to "200" range. It would have switched metal-film resistors for null tuning stability and accuracy, and it would have an additional amp for switching in 20dB of gain to the filter output to get wider dynamic range -- a solid 120dB. The unit would have battery power for great noise immunity. I was already into this active filter for the cost of some pots from Radio Shack, the opamps (which I had anyway), and a 3 pole, 4 position switch. I could spend a little more -- the second oscillator had cost *quite* a bit more than that. I went to a Michael's hobby supply, which is a nationwide chain, and got a great little 8" x 6" x 3" thin steel box with a lid to put everything in for $5 (I've since discovered that Michael's only have these boxes around Christmas, if they have them at all -- I got lucky). I ordered two 4-pole, 23-position switches from an eBay supplier in Hong Kong -- these switches are used in volume control attenuators for high quality analog audio preamps and such -- these weren't cheap, but they're very nice switches. These let me use 1% metal film resistors as the tuning elements for two of the three levels of tuning precision. This arrangement yields great tunability and stability. I had a couple of 500 ohm ten-turn pots on hand, bought years ago from a friend for just such an eventuality.These provide the tertiary level of tuning. Resistors I had to work out what sizes of resistors to use for the switches. I wanted the range capacitors to be easy values to buy and to sort for tolerance. I figured that caps with "10" values would be cheapest and easiest. Given the tuning frequency calculation, a pair of 10nF bridge caps and a 20nF (two 10s in parallel) pillar cap would tune to 1kHz with a total of 15.9k ohms for each of the bridge Rs and half that or 7.95k for the pillar R. Downscale, 200Hz would need about 79.6k ohms in the bridge Rs and 39.8k in the pillar R. At the far end, 2kHz, the bridge Rs would be 7.96k and the pillar R 3.98k. With the 23-position coarse and medium switches, and the ten-turn pots for the fine tuning, the two bridge Rs and the pillar R can be divided up for high resolution. The three sections of each branch are in series. If the medium and fine Rs can go to zero, then a minimum R for each branch of the coarse tuning at the high end of the range can be a bit under the needed R values. It was convenient to use a coarse R resistor in each branch as a limiting R in series with the switched steps, which sets the maximum tuned frequency a little over the "200" end of the scale, and raised the total series R to give the other end a frequency of just a little under the"20" end of the scale. The nicest thing would be to have the resistors scale to a log ratio so that the frequency steps would be spread evenly around the panel and knob. But that meant a strange assortment of resistors, and at low frequencies, fine tuning that wasn't fine enough, with the opposite problem at the other end of the scale, where the finest resistor granularity would be too coarse. So, I took the easy way out and used equal resistors for each step, resulting in a scale that isn't pretty, but works. The coarse tuning uses 3.24k ohms for each step of the bridge Rs and 1.62k ohms for each step of the pillar R. This is handy because these are standard 1% metal film resistor sizes -- and the two extra series resistors in each branch make the highest possible frequency about "245", with the lowest frequency about "19." For the medium, second level tuning, I needed resistor values that would total to somewhat more than a single step of the coarse tuning switch. I chose 165 ohms for the bridge Rs (23 * 165 = 3.795k) and half that or 82.5 ohms for the pillar R -- again these are standard 1% values. The 500 ohm pots were good as is and could be shunted if necessary for more resolution. Capacitors The only remaining problems were sorting the caps and adjusting for variances in cap value. I bought a few 5% caps in the 100nF, 10nF and 1nF sizes so that I could select for tolerance. I have a nice little 3-1/2-digit cap meter, and at these values it could get me close to 1% tolerances, matching the tolerances of the resistors. Even so, some variation might upset the cart. So I put a 1k pot in series with each of the three branches, and fiddled until I got a good null at both ends of the range and between ranges; you might have to add some resistance to one of the pots to get everything to work reliably. Here's the circuit diagram -- DDB, a contributor to the DIYAudio website has made a readable schematic for the filter. You can expand the image in most browsers for greater detail, or save the image to your desktop and expand it in any JPG viewer for easy viewing:  The coarse step values are 3.24k and 1.62k, and the medium step values are 165 and 82.5. These are all standard 1% values. But Patrick Turner raised the question of using less precise (and less expensive) parts. Resistors can be selected from the 5% series to 1% or better with almost any 3-1/2 digit DMM -- absolute accuracy isn't important, just the relative value of one to the next, and maintaining a very close 2:1 ratio for the bridge vs. pillar values. Convenient 5% resistor values are 3k and 1.5k for the coarse switch, and 150 and 75 for the medium switch. Carbon film resistors work fine in this application, but metal films are just better all around. My personal opinion is that sorting parts is a pain, and given that 1% metal films are readily available at reasonable cost, buying 10 or 20 times as many 5% carbon film resistors to get the ones you need ends up not being a big saving. One last issue is the fine tuning pots. The wire-wound 500 ohm pots I used are a little grainy for achieving nulls better than 100dB, but they're what I had -- just a couple of 200 ohm carbon pots may be all that's needed. When you're using a spectrum analyzer, you just need to get the fundamental largely out of the way -- 40dB seems to be good and 60dB of null is plenty. For reading with a meter, however, you want the fundamental gone, and it may take two stages of fine-tuning pots to hold nulls of more than -100dB, if you actually can hold that deep a null long enough. You might need carbon pots of 500 ohms and 100 ohms in series. With the current set-up, I can hold 100dB nulls for a short time, say 10 or 20 seconds -- long enough to read a meter. I can hold -110dB for a second or two -- not long enough for a meter to settle and get read. How well does it work? A great question and I have a great answer -- very well. Here's a spectrum of the oscillator in an HP 339:  Y-axis values are actually 20dB lower, due to added gain in the filter Note that the null is at an actual -100dBu, and that the 2nd and 3rd harmonics are actually at -120dB each. The hump in the noise floor at the null frequency is caused by the loss of feedback at the null, and accurately traces the shape of the noise curve for this amplifier and filter configuration. Here are some pictures of the construction:    I hope you're impressed by what a relatively simple active filter and some ordinary computer hardware and very good software can do. This is performance that can't be matched by an analog THD analyzer, and it works every bit as well at 10kHz as it does at 1kHz. Of course the bandwidth of the computer's ADC sampling system needs to be high enough to let you actually see important distortion products, and that is the primary limitation of this combination. My PC does 24-bit, 96kHz sampling, so I can get useful spectral products out to around 46kHz -- enough for working at 10kHz but not for 20kHz. If I had a 24- or 30-bit, 192kHz sound capability then the audio band would be fully covered. Actual measurements It needs to be said that it is a pain to have to mentally or physically calculate the RMS sum of the products; this filter could be improved by adding low frequency and high frequency stop band filtering for reading results with an RMS meter -- and that's doable, but reading those results also requires a lot more gain to make those 1ppm products big enough for most meters to measure -- say another 60dB of gain. I'm OK with just looking at the spectra and estimating the sum of the products, or just considering them individually. It's very nice to know which products are big and which aren't, so I find the spectrum display very useful. However, ARTA offers a solution -- you can tell it to calculate the RMS sum of the just distortion components, as well as the RMS sum of THD+noise, too. If you null the fundamental by precisely 60dB, then read the ARTA calculated values and divide by 1000, you have values equivalent to meter readings from a THD meter -- except that there's no noise filtering, of course. ARTA does let you filter out low-frequency hum and noise from the calculated values even though they are not removed from the spectrum display. 60dB is a good value for the null because it's high enough above the noise to keep the fundamental amplitude steady, and it's low enough to ensure that the PC sound system's residuals won't be a problem. And if you add gain from the filter's +20dB amp, be sure to include that too. As importantly, ARTA does give you a crude but effective way to control the measurement bandwidth -- change the sampling frequency -- I often want a 10kHz bandwidth for measuring the distortion+noise of 1kHz fundamentals, so as to exclude high-frequency noise that isn't relevant but still skews the numbers. I just change the sampling frequency to 22kHz, and the ARTA calculated values are cut off at about 10kHz; for a 20kHz bandwidth I elect to sample at 44.1 or 48kHz. The results have proven to be very close to RMS measured values with similar bandwidth. This amplifier filter system is quiet enough that the post-filter amp gain could be raised even more if the gear you're working with can benefit from the added resolution. Unlike with a THD analyzer, the spectrum analyzer's measurement floor isn't determined by the depth of the null of the fundamental, so you really can see extremely low levels of distortion. Update 4-13-2011 -- Larry Burk asked me a good question about an attenuator for the input, for the case of testing power amps at high levels. This circuit likes to be driven from a relatively low-Z source -- the output of a power amp is good. So is the output of an opamp. The circuit is somewhat sensitive to source Z, both in level and Q. For example, at 1kHz, a 600 ohm source causes a drop in the upper passband level of 0.28dB and softens the Q somewhat. As a general rule, the lowest resistance at the input will be about 3/4 of one bridge arm's total resistance. At 1kHz, for example, one bridge arm resistance is about 15.9k, making the input resistance roughly 12k. As frequency decreases, the input resistance increases significantly, so at the bottom end of a range, the resistance will be as much as 5X higher. For high signal levels like from big power amps, I recommend using a two-resistor voltage divider with a bottom leg of 100 ohms, and an upper leg suitable to get the division ratio you need -- but it may be important to add some capacitance across the bottom leg resistor to compensate for the residual shunt C around the upper leg resistor, making a frequency-compensated attenuator that keeps the frequency response flat out to 100kHz. Try to keep filter set-level outputs in the 0.5 to 1VRMS range when using a PC spectrum analyzer. As long as the voltage divider is reasonably precise, you can monitor the input to the attenuator with a voltmeter and you'll know the input level to the filter by definition. ### Update 12-21-2011 -- Up until recently, I had been using the on-board sound input capability of my PC to do the Analog-to-Digital Conversion (ADC) work. But I was limited in upper bandwidth by its maximum sampling frequency of 96kHz, and the linearity was a little suspect. I wanted to look at higher frequency products. Having an ADC with 192kHz sampling would allow reasonable estimates of at least low-order distortion products out to perhaps 80kHz, letting me look at fundamentals as high as 20kHz. After looking at relatively inexpensive "sound cards," I chose an E-MU 0204 USB adapter. It turned out to have lower noise and distortion than my on-board system. Update 6-7-2012 -- I've had lingering questions about linearity of the EMU 0204's ADC. The measurements made with the Active Twin-T notch filter can't be any better than the linearity of the ADC used with it. I have unwittingly been plagued by ARTA choosing the wrong driver for the EMU 0204 on start-up; the idiot using the software didn't notice that this was happening. This was causing all kinds of strangeness. So I made sure that the ASIO driver was loaded in ARTA and connected my precision HP 353A attenuator to the HP 339A oscillator output, with the output of the 353A connected to the EMU's line input, giving me a combined attenuation range of over -150dB -- that's plenty. The 353A is rated for a maximum error of +/- 0.5dB over its whole range, and I know that the attenuator in the 339A is better than 0.2dB over its range. I set the ARTA software to a reference level of 0dBV using a source of precisely 1VRMS (it's good to have an accurate AC voltmeter -- min is an HP 3458A 8-1/2 digit DMM) at 1kHz from the 339A oscillator. Then I stepped the attenuation in -10dB steps. Here are my results, in short form. I'll annotate each spectrum plot below it. The first is at a signal level of -60dB:  Here is the plot for -120dBV:  Here is the same plot up close and personal:  Here's the plot for -130dBV:  Finally, just to impress, here's a broad spectrum plot at -140dBV:  Now it is possible that the combined errors of the two attenuators and the non-linearity of the ADC combine to null each other out. If so, that's a happy result and I'll take it. ### I've done some evaluation of the EMU, and have begun to ponder the question: Where is the residual distortion coming from? In my test setup, there are three sources of distortion -- the oscillator, the Twin-T filter, and the EMU. I don't have a distortionless oscillator. Using the digital oscillator in the ARTA analyzer program, fed thru the EMU's DAC, isn't the solution -- distortion is low, but not low enough. My HP 239 oscillator has low distortion, as does the oscillator in the HP 339 Analyzer -- they are the lowest distortion oscillators I have. But how low is their distortion? To properly evaluate the residual distortion of the Twin-T filter and of the EMU ADC, I should have an oscillator with distortion products lower than -140dB, and lower if possible. Well, that's not going to happen right now, although my friend David Barber is working on it. All I can say is, "stay tuned." What I have done is make some spectra of the 10kHz output from the HP 239, using various combinations of level settings and the other gear. The descriptions follow each spectrum. I chose 10kHz for examination because, although the oscillator has lower distortion at 1kHz, so do the Twin-T and the EMU. 10kHz stresses everything just a bit more. I chose to use 1VRMS as the highest output from the 239, because that is the level that the EMU is good with at moderate gain in its input amplifier. With these settings, the EMU clips at an input of a bit over 3dBV, so 0dBV is comfortably under the full-scale input, but high enough to assure lowest ADC distortion. I tried to find the best distortion+noise vs. level trade-off, but that's really hard to evaluate when everything in the signal chain is near its lowest levels anyway. This, as Paul Klipsch used to say, is "milking mice." What can be expected of the EMU, given its 24-bit resolution? that's a dynamic range of 144dB! But noise and distortion seriously limit that maximum performance, including contributions from the input amplifier. It's an open question as to what can be expected here from any of the gear. Spectrum 1 --  This is the 239 fed directly into the EMU. The indicated spectrum levels are referred to 0dBV = 1VRMS. The 239's attenuator is set to 1V, but that's its level into a 600 ohm load, so the variable knob is adjusted -6dB for 1V out. The 239's output feeds a passive 30k ohm attenuator pot (set very near full output), which feeds the EMU. The 2nd and 3rd harmonics are near -100dB, which is the distortion of the EMU's total system -- input amp plus ADC -- at this input level; the HP 239 is lower. So, these distortion levels are the floor for the E-MU at near-full-scale input. Note the rise in the noise floor as frequency increases. I speculate that this is an artifact of the noise-shaping filtering of the E-MU's sigma-delta converter. ARTA's calculated THD of 0.0021% (-94dB) looks to be right on compared to the product levels. Spectrum 2 --  This is the same as 1 except that the output attenuator of the 239 is set to 0.1V, a drop of 20dB in the input to the EMU. The distortion levels have decreased by almost 30dB, not the expected 20dB, which is counter-intuitive, because the distortion of ADCs goes up as level goes down. So, this could be the lowered distortion of the EMU's input amp at the 20dB lower level, bringing us near the floor for the EMU as a whole -- but we also could be closing in on the oscillator's distortion. ARTA's calculated THD of 0.0041% looks all wrong compared to the levels of the products on-screen -- I have no explanation. Everything above 40kHz seems to be spurious junk -- there is some 50kHz 5th harmonic signal there but it's being modulated by line and/or other noise, and its true level is not visible. The next question is: Do the Twin-T's amplifiers add distortion? So first, a spectrum of the Twin-T in set-level mode, then a spectrum in filter mode: Spectrum 3 --  This is the same as Spectrum 1 with the Twin-T in the chain. The Twin-T is in set-level mode, so there is no filtering. There are slight differences in the relative levels of the 2nd and 3rd harmonic products compared to 1, but the overall distortion is about the same. So the Twin-T isn't adding much, if anything. Spectrum 4 --  Here, the Twin-T is in filter mode, as can be seen by the low level of the fundamental. The distortion product levels are referred to the 0dBV level. The low fundamental makes ARTA's calculation of the THD hard to refer to the 0dBV level -- but it calculates out about right for a THD of about 0.0005% -- pretty good for a 10kHz oscillator. What matters are the levels of the products compared to the levels in Spectrum 3. The levels have dropped by 10dB or more, which means that the EMU's distortion has gone down, but not nearly as much as in Spectrum 2, indicating that we are seeing either the residual of the HP 239 oscillator or the residual of the Twin-T filter, or both. Which is it? Spectrum 5 --  This is the same as 4, but the oscillator's output attenuator is dropped 10dB -- this does not change the distortion relative to the level, it just changes the level. If the distortion is primarily from the Twin-T, then the lower level should result in more than a 10dB drop in the levels of the products. If the distortion is primarily from the oscillator, then the products should drop by the same amount as the attenuation of the output -- 10dB. As can be seen, the products do drop almost exactly 10dB, indicating that we are seeing the 10kHz distortion of the HP 239. Given the outstanding linearity of the EMU's ADC, this result means that the Active Twin-T and the EMU 0204 together offer an accurate view of very low distortion levels -- in the area of -130dB or lower -- in oscillators and other electronic gear. Update 10-28-2012 -- Simpler configuration for a few frequencies I've had some requests for more information about parts values and possible modifications, and I've been thinking about the usability of the filter. I find I mainly use it at 1kHz and at 10kHz, with other frequencies only very rarely. The design is easily simplified to do just a few frequencies with much less elaborate switching of the tuning resistors. A possible penalty is not having much tuning range, but most oscillators that will be used as sources can be tuned as well. Having four frequencies, for example, would require twelve 1% resistors, at most twelve capacitors (but probably fewer, depending on the frequencies chosen) and three 10-turn wirewound pots -- these pots should have values 5% or less of the R value in the frequency formula. The detailed description above covers the formula for tuning frequency, so choosing resistors and capacitors is straightforward. In general, the resistor value R shouldn't be under about 2kohms, but higher is better to avoid source loading; unless the cap value C is then too small -- this is a bigger issue at high frequencies, as a little work with a spreadsheet or calculator will show. A C value that is too small will be significantly changed by the inevitable stray C of the parts and wiring, making use at 50 or 100kHz, for example, a challenge. ### |
|
|